__________
专题18革新型与新概念综合问题
【考试知识点1】几何综合探究类阅读理解问题
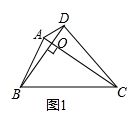
【例1】（2019·甘肃天水）如图1，对角线互相垂直的四边形叫做垂美四边形．
（1）定义理解：如图2，在四边形ABCD中，AB=AD，CB=CD，问四边形ABCD是垂美四边形吗？请说明理由；
（2）性质探究：如图1，四边形ABCD的对角线AC、BD交于点O，AC⊥BD．
试证明：AB2+CD2=AD2+BC2；
（3）解决问题：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连结CE、BG、GE．已知AC=4，AB=5，求GE的长．
【答案】（1）四边形ABCD是垂美四边形．理由见分析.（2）见分析.（3）GE=
．
【分析】（1）四边形ABCD是垂美四边形．理由如下：
∵AB=AD，∴点A在线段BD的垂直平分线上，
∵CB=CD，∴点C在线段BD的垂直平分线上，
∴直线AC是线段BD的垂直平分线，
∴AC⊥BD，即四边形ABCD是垂美四边形；
（2）如图1，
∵AC⊥BD，∴∠AOD=∠AOB=∠BOC=∠COD=90°，
由勾股定理得，AB2+CD2=AO2+BO2+DO2+CO2=AD2+BC2，
∴AD2+BC2=AB2+CD2；
（3）连接CG、BE，
∵∠CAG=∠BAE=90°，
∴∠CAG+∠BAC=∠BAE+∠BAC，即∠GAB=∠CAE，
在△GAB和△CAE中，
，
∴△GAB≌△CAE（SAS），
∴∠ABG=∠AEC，又∠AEC+∠AME=90°，
∴∠ABG+∠AME=90°，即CE⊥BG，
∴四边形CGEB是垂美四边形，
由（2）得，CG2+BE2=CB2+GE2，
∵AC=4，AB=5，∴BC=3，CG=4
，BE=5，
∴GE2=CG2+BE2-CB2=73，∴GE=．
【名师点睛】（1）依据垂直平分线的断定定理证明即可；（2）依据垂直的概念和勾股定理解答即可；
（3）依据垂美四边形的性质、勾股定理、结合（2）的结论计算．本题考查的是正方形的性质、全等三角形的断定和性质、垂直的概念、勾股定理的应用，正确理解垂美四边形的概念、灵活运用勾股定理是解题的重点．
【变式1-1】（2019·甘肃白银）阅读下面的例题及点拨，并解决问题：
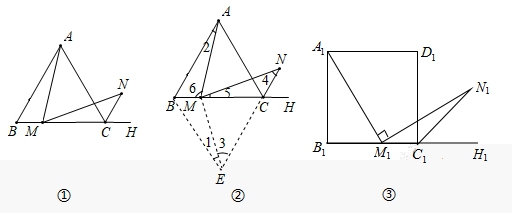
例题：如图①，在等边△ABC中，M是BC边上一点（不含端点B，C），N是△ABC的外角∠ACH的平分线上一点，且AM=MN．求证：∠AMN=60°．
点拨：如图②，作∠CBE=60°，BE与NC的延长线相交于点E，得等边△BEC，连接EM．易证：△ABM≌△EBM（SAS），可得AM=EM，∠1=∠2；又AM=MN，则EM=MN，可得∠3=∠4；由∠3+∠1=∠4+∠5=60°，进一步可得∠1=∠2=∠5，又由于∠2+∠6=120°，所以∠5+∠6=120°，即：∠AMN=60°．
问题：如图③，在正方形A1B1C1D1中，M1是B1C1边上一点（不含端点B1，C1），N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点，且A1M1=M1N1．求证：∠A1M1N1=90°．
【答案】见分析.
【分析】延长A1B1至E，使EB1=A1B1，连接EM1、EC1，
如图所示：
则EB1=B1C1，∠EB1M1=90°=∠A1B1M1，
∴△EB1C1是等腰直角三角形，
∴∠B1EC1=∠B1C1E=45°，
∵N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点，
∴∠M1C1N1=90°+45°=135°，
∴∠B1C1E+∠M1C1N1=180°，
∴E、C1、N1三点共线，
在△A1B1M1和△EB1M1中，
，
∴△A1B1M1≌△EB1M1（SAS），
∴A1M1=EM1，∠1=∠2，
∵A1M1=M1N1，∴EM1=M1N1，∴∠3=∠4，
∵∠2+∠3=45°，∠4+∠5=45°，∴∠1=∠2=∠5，
∵∠1+∠6=90°，∴∠5+∠6=90°，
∴∠A1M1N1=180°﹣90°=90°．
【名师点睛】此题是四边形综合题目，考查了正方形的性质、全等三角形的断定与性质、等腰直角三角形的断定与性质、等腰三角形的断定与性质、三角形的外角性质等常识；本题综合性强，熟练学会正方形的性质，通过作辅助线架构三角形全等是解本题的重点．
【变式1-2】（2019·湖北咸宁）概念：有一组邻边相等且对角互补的四边形叫做等补四边形．
理解：
（1）如图1，点A，B，C在⊙O上，∠ABC的平分线交⊙O于点D，连接AD，CD．
求证：四边形ABCD是等补四边形；
探究：
（2）如图2，在等补四边形ABCD中，AB=AD，连接AC，AC是不是平分∠BCD？请说明理由．
运用：
（3）如图3，在等补四边形ABCD中，AB=AD，其外角∠EAD的平分线交CD的延长线于点F，CD=10，AF=5，求DF的长．
【分析】（1）如图1，∵四边形ABCD为圆内接四边形，
∴∠A+∠C=180°，∠ABC+∠ADC=180°，
∵BD平分∠ABC，∴∠ABD=∠CBD，∴
，∴AD=CD，
∴四边形ABCD是等补四边形；
（2）AD平分∠BCD，理由如下：
如图2，过点A分别作AE⊥BC于点E，AF垂直CD的延长线于点F，
则∠AEB=∠AFD=90°，
∵四边形ABCD是等补四边形，∴∠B+∠ADC=180°，
又∠ADC+∠ADF=180°，∴∠B=∠ADF，
∵AB=AD，∴△ABE≌△ADF（AAS），∴AE=AF，
∴AC是∠BCF的平分线，即AC平分∠BCD；
（3）如图3，连接AC，
∵四边形ABCD是等补四边形，∴∠BAD+∠BCD=180°，
又∠BAD+∠EAD=180°，∴∠EAD=∠BCD，
∵AF平分∠EAD，∴∠FAD=
∠EAD，
由（2）知，AC平分∠BCD，
∴∠FCA=∠BCD，∴∠FCA=∠FAD，
又∠AFC=∠DFA，∴△ACF∽△DAF，
∴
，即
，∴DF=5
﹣5．
【名师点睛】本题考查了新概念等补四边形，圆的有关性质，全等三角形的断定与性质，角平分线的断定，相似三角形的断定与性质等，解题重点是要可以通过自主学习来进行探究，运用等．
【考试知识点2】代数类新概念及阅读理解型问题
【例2】（2019•自贡）阅读下列材料：小明为了计算1+2+22+…+22017+22018的值，使用以下办法：
设S=1+2+22+…+22017+22018①，
则2S=2+22+…+22018+22019②，
②–①得2S–S=S=22019–1，
∴S=1+2+22+…+22017+22018=22019–1.
请仿照小明的办法解决以下问题：
（1）1+2+22+…+29=__________；
（2）3+32+…+310=__________；
（3）求1+a+a2+…+an的和（a＞0，n是正整数），请写出计算过程．
【答案】（1）210–1；（2）；（3）a=1时，S=n+1；a≠1时，S=．
【分析】（1）设S=1+2+22+…+29①，
则2S=2+22+…+210②，
②–①得2S–S=S=210–1，
∴S=1+2+22+…+29=210–1；
故答案为：210–1；
（2）设S=3+3+32+33+34+…+310①，
则3S=32+33+34+35+…+311②，
②–①得2S=311–1，
所以S=，
即3+32+33+34+…+310=；
故答案为：；
（3）设S=1+a+a2+a3+a4+…+an①，
则aS=a+a2+a3+a4+…+an+an+1②，
②–①得：（a–1）S=an+1–1，
a=1时，不可以直接除以a–1，此时原式等于n+1；
a≠1时，a–1才能做分母，所以S=，
即1+a+a2+a3+a4+…+an=.
【名师点睛】依据题目给出的信息，提炼解题办法．认真察看、仔细考虑，善用联想，借助类比的办法是解决这种问题的办法．
【变式2-1】（2019•随州）若一个两位数十位、个位上的数字分别为m，n，大家可将这个两位数记为
，易知=10m+n；同理，一个三位数、四位数等均可以用此记法，如
=100a+10b+c．
【基础练习】
（1）解方程填空：
①若+
=45，则x=__________；
②若
–
=26，则y=__________；
③若
+=，则t=__________；
【能力提高】
（2）交换任意一个两位数的个位数字与十位数字，可得到一个新数
，则+肯定能被__________整除，–肯定能被__________整除，•–mn肯定能被__________整除；（请从大于5的整数中选择适合的数填空）
【探索发现】
（3）北京时间2019年4月十日21时，人类拍摄的首张黑洞照片问世，黑洞是一种引力很大的天体，连光都逃脱不了它的束缚．数学中也存在有趣的黑洞现象：任选一个三位数，需要个、10、百位的数字各不相同，把这个三位数的三个数字按大小重新排列，得出一个最大的数和一个最小的数，用得出的最大的数减去最小的数得到一个新数（比如若选的数为325，则用532–235=297），再将这个新数按上述方法重新排列，再相减，像如此运算若干次后必然会得到同一个重复出现的数，这个数称为“卡普雷卡尔黑洞数”．
①该“卡普雷卡尔黑洞数”为__________；
②设任选的三位数为（可以设a＞b＞c），试说明其均可产生该黑洞数．
【答案】（1）①2．②4．③7．（2）11；9；10．
【分析】（1）①∵=10m+n，
∴若+=45，则10×2+x+10x+3=45，
∴x=2，
故答案为：2．
②若–=26，则10×7+y–（10y+8）=26，
解得y=4，
故答案为：4．
③由=100a+10b+c，及四位数的类似公式得
若+=，则100t+10×9+3+100×5+10t+8=1000×1+100×3+10t+1，
∴100t=700，
∴t=7，
故答案为：7．
（2）∵+=10m+n+10n+m=11m+11n=11（m+n），
∴则+肯定能被11整除，
∵–=10m+n–（10n+m）=9m–9n=9（m–n），
∴–肯定能被9整除．
∵•–mn=（10m+n）（10n+m）–mn=100mn+10m2+10n2+mn–mn=10（10mn+m2+n2）
∴•–mn肯定能被10整除．
故答案为：11；9；10．
（3）①若选的数为325，则用532–235=297，以下根据上述规则继续计算，
972–279=693，
963–369=594，
954–459=495，
954–459=495，…
故答案为：495．
②当任选的三位数为时，首次运算后得：100a+10b+c–（100c+10b+a）=99（a–c），
结果为99的倍数，因为a＞b＞c，故a≥b+1≥c+2，
∴a–c≥2，又9≥a＞c≥0，
∴a–c≤9，
∴a–c=2，3，4，5，6，7，8，9，
∴首次运算后可能得到：198，297，396，495，594，693，792，891，
再让这类数字经过运算，分别可以得到：
981–189=792，972–279=693，963–369=594，954–459–495，954–459=495…，
故都可以得到该黑洞数495．
【名师点睛】本题是较为复杂的新概念考试试题，题目设置的问题较多，但解答办法大同小异，总体中等困难程度略大．
